Numerical explorations of strong-field gravity

Background

Einstein’s theory of general relativity (GR) has been remarkably successful over the past century, correctly predicting the existence of black holes, gravitational waves, the cosmic microwave background, and many other fascinating exotic phenomena. GR’s ability to describe these systems derives in part from the complexity of its equations, which makes extracting future predictions quite tricky.

In the sections below I briefly outline a couple of projects which aim to explore how gravity works (according to GR) in the strong-field regime, where the equations are pushed to their limits. To be specific, below we consider the structure of spacetime inside of black holes, and various formal similarities between the nonlinear behavior of gravity and turbulence in fluid mechanics.

What’s inside of black holes?

Paper: The rotating black hole interior: Insights from gravitational collapse in AdS_3 spacetime
Authors: Alex Pandya, Frans Pretorius

It is widely believed that black holes have an exterior geometry well-described by the famous Kerr solution to the Einstein equations of GR¹. This notion is closely tied to the fact that any special features (e.g. a ‘bump’ in the horizon) either fall in, or, if they’re moving fast enough not to fall in, rapidly escape and fly off to infinity (the no-hair theorem).

The same behavior does not occur inside the black hole. There, escape is by definition impossible, so the interior geometry is sensitive to the stuff that fell in. The Kerr solution is very special (it describes a black hole which never formed – by assumption it was always just there, spinning along in an otherwise empty universe) and thus does not describe the interior geometry of a real black hole formed by the messy collapse of a large star.

In order to investigate the interior structure of a black hole formed from the gravitational collapse of matter, I (along with my advisor Frans Pretorius) simulated such a collapse numerically in the context of a particular toy model². We found that the structure of the black hole interior in this case depends strongly on the black hole’s spin; the precise dependence is summarized in the figure below.

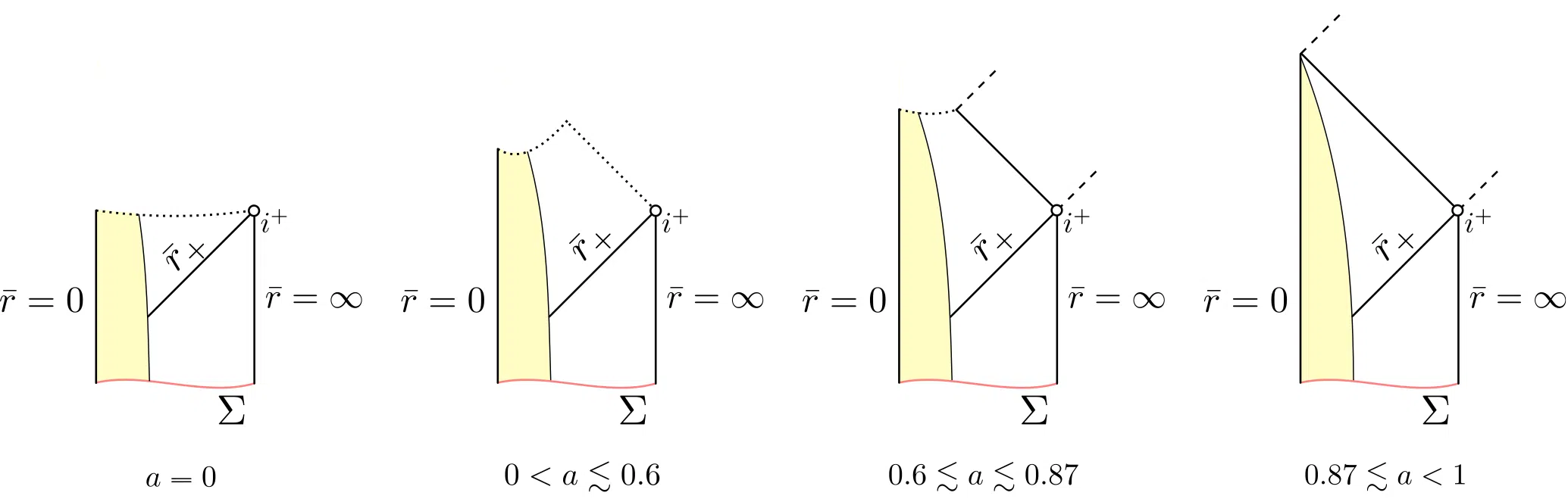
We also found the development of a “gravitational shock-wave”, where an infalling observer would be crushed by a very rapid increase in spacetime curvature before they reach the center of the black hole (which in this context may not contain a singularity if the hole is spinning rapidly enough).

Can gravity act like a fluid?

Paper: Dynamics of a nonminimally coupled scalar field in asymptotically AdS_4 spacetime
Authors: Alex Pandya, Justin L. Ripley

GR and relativistic fluid mechanics share a similar mathematical structure: namely, they are both systems of coupled hyperbolic partial differential equations. A direct result of this fact is that both frameworks can lead to the formation of singularities: in GR, they arise in the center of black holes; in fluid mechanics, they arise in droplet formation or in inviscid shocks.

In this paper we investigated a formal similarity between the dynamics of a scalar field coupled to gravity and a viscous fluid. It turns out that both can be written with stress-energy tensors of the same form, provided one identifies a particular derivative of the scalar field with the fluid’s flow velocity. We also study the turbulent instability of anti-de Sitter (AdS) spacetime viewed through this perspective.

We find that the mapping from scalar field to viscous fluid does imply fluid-like behavior in the scalar; in fact, simple metrics indicate that the ‘scalar fluid’ is highly pathological (i.e. the energy density can dynamically change sign). That said, we do observe interesting dynamics in the turbulent instability of AdS as a function of the non-minimal coupling between the scalar field and gravity.

Footnotes